Click Images to View in Full Size.
Courtesy of author and case researcher John Gannon.
—
Murder Night Report:
https://www.williamherbertwallace.com/wp-content/uploads/2020/08/McFall-Report.pdf
Post-Mortem Report:
https://www.williamherbertwallace.com/wp-content/uploads/2020/08/Post-Mortem-Report.pdf
—
Committal Trial:
Slightly blurry. Click to enlarge and zoom in to read the material.
—
Diagrams & Scrawling:
—
Main Trial:
Transcribed (John Gannon):
JOHN EDWARD MACFALL SWORN. EXAMINED BY MR HEMMERDE.
1732. Is your name John Edward Wheatley MacFall, and you are Professor of Forensic Medicine in the University of Liverpool and (?) in Medical Jurisprudence in the Universities of Glasgow, Edinburgh, Manchester and Birmingham? I am.
1733. On the 20th January last were you called in to 29 Wolverton Street, and did you arrive at about 9.50? I did.
1734. When you arrived what did you see in the front parlour? I saw the dead body of a woman lying upon the hearthrug face downwards, and the face was turned to the left. The left arm was extended, and the right arm was by the side of the body. The body was fully clothed and lay diagonally across the hearthrug. The head was by the corner of the rug nearest to the door. The head was badly bettered in on the left side above and in front of the ear, where there was a large open wound approximately half an inch by three inches, from which bone and brain substance was protruding. At the back on the left side of the head, there was a great depression of the skull, with severe wounds. The matted hair obscured the detail of the wounds, which I shall be able to describe later. There was a large patch of blood clot on the edge of the hearthrug on the side at the end nearest the sideboard, and a large patch of blood clot on the brain substance and bone, and pieces of bone by the edge of the hearthrug towards the door on which the head was lying. The hands were quite cold; the lower arms were cold, but the upper arms and the body was warm. Rigor mortis, the stiffening that follows death, was present in the upper part of the left arm and the neck. The head was turned to the left and fixed by post-mortem rigidity of the neck by about one o’clock that is approximately two hours afterwards.
1735. Three hours after? Yes, three hours afterwards; that was practically when I was leaving, and I was watching the body in between and watching the process of this stiffening; it was by this time, about one o’clock, the post-mortem rigidity had extended to the right arm and the right leg, but on my first observation when I noted that the neck was stiff and the upper part of the left arm was stiff my opinion then was that death had taken place quite four hours before ten o’clock. On further examination of the body there was a little blood staining of the hair. There was nothing clenched in the hands, and nothing beneath the fingernails.
1736. Before you go on, you say you formed the view of four hours. Could you give a definite minimum that it must have been? A certain time? There is always a certain amount of possibility one way or the other, but the opinion I formed then was that it was over four hours since this woman had been dead.
1737. MR JUSTICE WRIGHT: That is at ten o’clock at night? That would bring it back from ten o’clock to six o’clock.
1738. MR HEMMERDE: What would you regard as the possible margin of error in that calculation? It could not possibly be in this case more than an hour; it is not possible, because post mortem rigidity is not merely beginning, it has begun and has progressed to a certain extent in the neck and in the arm.
1739. MR JUSTICE WRIGHT: One hour’s error would bring it to seven o’clock: half an hour’s error would bring it to half-past six? Yes, but there is the other way, and I formed the opinion then it was four hours or more.
1740. MR HEMMERDE: Now, will you go on? You just said that there was some blood staining of the hands, nothing clenched in the hands and nothing beneath the finger nails? I noticed particularly the blood clot. One gets a certain amount of experience, having seen a number of cases, and you form an opinion, immediately you see a blood clot, on its age. This is only approximate; it is by no means definite: it is an opinion that can be formed from a consideration of post-mortem rigidity, but still it is a good point. This clot, instead of being the bright red that one sees in blood that has been shed half an hour to an hour, had the dark appearance that one sees in a blood clot that has been shed two or three hours. I cannot go beyond that. It was getting a darker red. There was also serum, but that is very little to go upon, because the liquid portion of the blood, the serum, runs out very soon, but still there was a serum exudation. It is the general appearance of the clot. As I have to allude later to this exudation of serum, I note here that there was serum exudation in this clot on the floor.
1741. Did you notice blood splashes? There were blood splashes. I have here bits of paper that I had in my pocket at the time, and these are a very rough sketch of what I have already described.
1742. What are these? You made a sketch, I think, first of all of the room, the body and the furniture? Yes.
1743. They probably would be very valuable? Yes, they were made at the time, or very soon after.
1744. May I see one of the room?
MR ROLAND OLIVER: This is new evidence. I think we should have had an opportunity of seeing these before now.
THE WITNESS: It is not new evidence.
MR ROLAND OLIVER: The right of the prisoner in a criminal case is to see them at the time the evidence is given or at the time of the committal.
MR JUSTICE WRIGHT: Was any reference made to them at the police court?
THE WITNESS: No.
MR JUSTICE WRIGHT: If you want them (the case will not finish today), you can see them.
MR ROLAND OLIVER: I am not saying it to make a grievance, but I think we should have had them.
MR JUSTICE WRIGHT: You can see them.
THE WITNESS: I stated in my evidence that I had given them, and it was also stated by other witnesses that I had been seen making sketches.
1745. And nobody asked to look at them? No, my Lord, they did not.
MR HEMMERDE: I do not think it will embarrass anybody, but I want to get it on the Note.
1746. MR JUSTICE WRIGHT: We must exhibit it now. What is it? It is the position of the chairs and the body roughly, as I saw them.
MR JUSTICE WRIGHT: That will be Exhibit 56.
THE WITNESS: These are in the form of notes which I referred to.
1747. MR HEMMERDE: In this sketch you have marked here with a cross, two blood clots? Yes.
1748. And one brain tissue? Yes, blood and brain tissues.
1749. You sketch the position of the body as you found it, and you put in the position of the chairs? Yes.
1750. What time? It is marked at 10 pm? Yes, soon after my arrival, about 10 pm.
1751. You have actually put the time on it in ink – “10 pm”? That was afterwards, when I was making a note upon it. I first made the sketch in pencil and then made the note upon it with my description after. That was the time it was written.
1752. When was the note made with reference to the sketch, the ink? I think I had that book and wrote it at the same time. The idea was to sketch it in pencil and put the other details in, in ink.
1753. And do the details here as regards the position of the chairs represent what you saw at ten o’clock? Exactly what I saw, that is one chair.
1754. In front? Yes, as I saw it.
1755. MR JUSTICE WRIGHT: Let me see it. (Same handed to his Lordship). Is the chair in front of the sideboard? Yes, that is how I saw it, a chair in front of the sideboard.
MR JUSTICE WRIGHT: Members of the jury, you had better look at it (Same handed to jury). It agrees with the photo, apparently.1756. MR HEMMERDE: Yes, my Lord. (To the witness): I would like you to look at the photograph that has been produced, photograph No 6. (Same handed to witness). Yes, that is it, approximately, but there are one or two things different here. There is a music stand just about the corner of the rug, the right hand corner by the aspidistra there.
1757. Look at No 7 and see if you can find it there? Yes, but it had been moved, evidently.
1758. You think that had been moved? Yes. This is only approximate. The mackintosh is quite different to when I saw it there.
1759. The chair is in the same position, approximately: the music stand you think is slightly moved? Yes. In No 6, it is in proper position: in No 7, it is not.
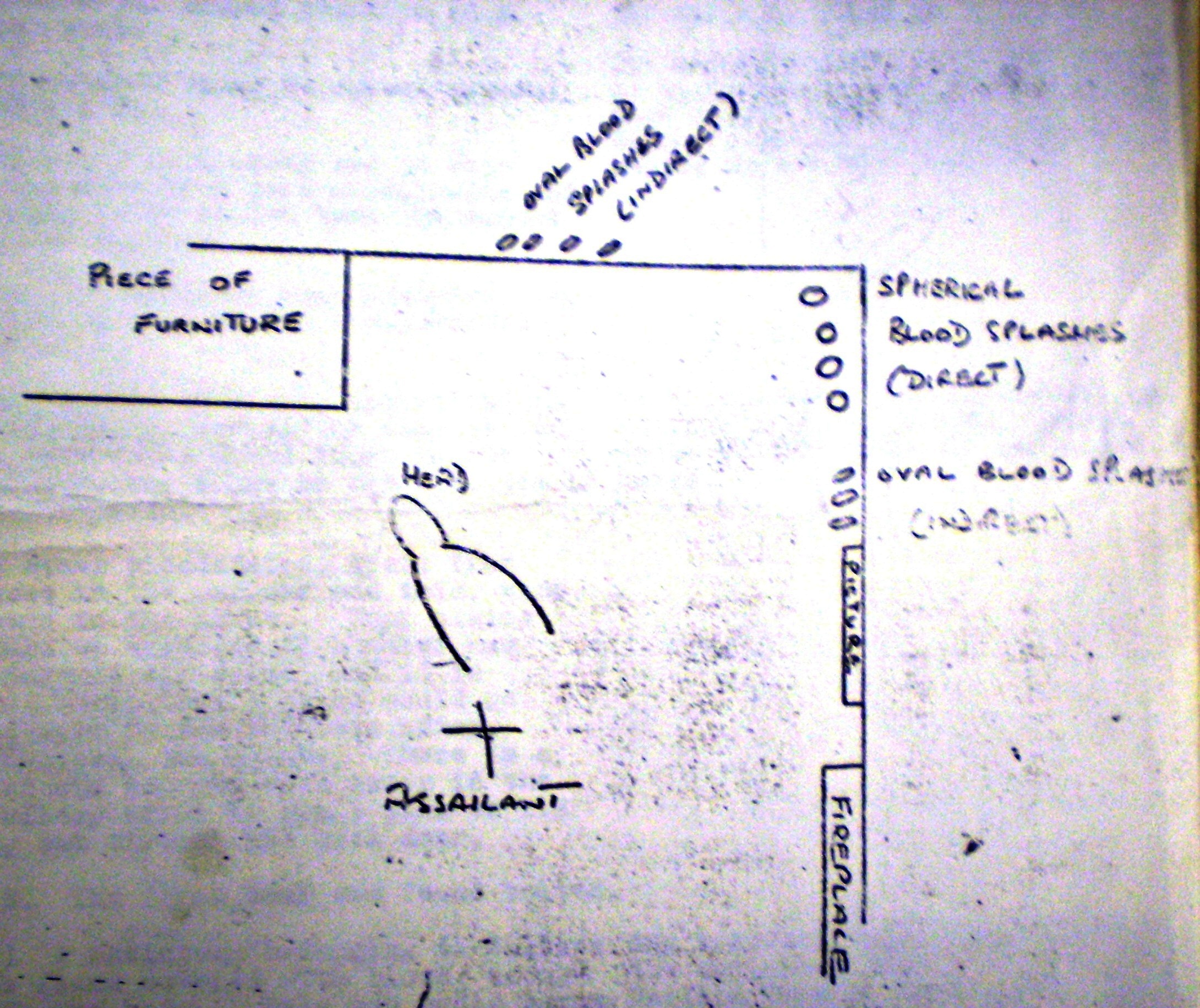
1760. I think we can now come to what I was going to ask you about blood splashes on the wall and about the place? There were a large number of typical blood splash marks in a circle from the edge of the sideboard: that is the edge of the sideboard as seen in No 7, the right hand side of the sideboard, and as seen in my sketch. These are notes and there is a rough sketch of this. (Handing same).
1761. These are rough marks of the blood? Yes. I can describe them, perhaps, better than you can see them there.
1762. MR JUSTICE WRIGHT: Where are they, on the sideboard or walls or where? I will explain that.
MR HEMMERDE: If your Lordship has a magnifying glass, your Lordship can see them in the photograph.
THE WITNESS: I can lend your Lordship one. It is rather important that the direction of these should be seen. You can see two definite little specks: one is showing in the space at the back of the chair, and there is one just above the violin case. If you look at those two splash marks you will see they give a definite direction. They are what we call soda-bottle marks. When blood is projected through the air it travels as a sphere, and when it touches a surface the top sticks and the bottom tumbles and gives it its appearance. You can always tell the direction in which it comes from the appearance of these so-called soda-bottle marks.
MR JUSTICE WRIGHT: Members of the jury, you will see the marks. There is one just above the arm of the chair and there is one in that little gap.
THE WITNESS: That is so. There are one or two very small ones on the picture above, again; they all give direction, but the two more definite blood marks are on the top of the sideboard. They are not shown in the photograph, but they are shown in my sketch on the top of the sideboard just at the corner, and their direction goes towards the picture.1763. There are two on the wall? There are more than two; there are more behind my Lord. The direction is from in front of the sideboard a little going round the corner. No 6 shows you again, quite definitely under the picture: there the marks are round.
1764. There are a lot of them? Yes, and they are all round.
1765. I can count seven? They are all round, and from that one deduces that the blood has struck it directly, not glancing, but a direct hit, as it were. If you go still further round you will see on the side of the wall by the fireplace again some blood marks and they are not direct hits. They are shown tumbling over the top again.
1766. Which are they? There is one at the top in the circle at the side of the fireplace and just opposite to the arm of the chair.
1767. There is one I see inside at the end of the arm? Yes.
1768. And one above that? Yes.
1769. Slightly to the left of it above? Yes.
1770. And then there are two above the arm of the chair? Yes, and there are a lot on the picture.MR JUSTICE WRIGHT: Are there?
MR HEMMERDE: Yes, my Lord, 20 or 30.
THE WITNESS: None of those that you can see on the picture or on the wall behind the chair show any diagonal direction, as it were; they are all direct.
1771. Mr Justice Wright: You mean none of those shown in the photograph show any direction? Only the two.
1772. The two beside the fireplace? Yes. There are a few of those which are as high as 7 feet, I think. In photograph No 7 even above the picture you can see small ones, but the majority that we have been examining now are about 4 feet high, or approximately that
1773. MR HEMMERDE: Could you form a view as to where the blow was struck, where the deceased was at the time? Yes. If you take these and concentrate them upon a central position, they concentrate fairly definitely in front of the chair.
1774. The chair by the side of the fire? The armchair on which is the violin case.
1775. MR JUSTICE WRIGHT: Which armchair? The armchair on the left of the fireplace.
MR HEMMERDE: Your Lordship sees the armchair in the photograph No 7?
MR JUSTICE WRIGHT: Yes, but it is not by the fireplace.
THE WITNESS: The chair is by the fireplace.
MR JUSTICE WRIGHT: Yes, the chair is, but not the violin case.
MR HEMMERDE: The case, not the stand.
1776. MR JUSTICE WRIGHT: Was the case lying on the chair? When I saw it, the case was on the chair.
1777. Then you say she was struck in front of the armchair to the left of the fireplace, the chair on which is the violin case? Yes.
1778. She was standing somewhere near the fireplace? I think it is a little too low to be standing.
1779. What do you deduce from that? It is suggested to my mind that the person had been sitting on that chair with the head a little forward slightly turned to the left as if talking to somebody.
1780. What about the violin case: would not that be in the way? No, the violin case would not be in the way if she sat in the chair. I sat in the chair, and that did not interfere, if she was sitting in the front of the chair.
1781. You think she was sitting in front of the chair turned a little forward towards the fireplace. Yes. If you put the head in that position and imagine it in that position as the source of this blood, the blood goes exactly in every direction and fits in there exactly with the appearances found.
1782. MR HEMMERDE: Was there any blood on the seat of the chair? I did not see any.
1783. That would rather bear out your theory? Yes.
1784. MR JUSTICE WRIGHT: Why? Because if the person is seated on it there would not be any.
1785. You mean if she had been anywhere else, the blood would have got on to the seat of the chair? Yes, my Lord. There were also a very few small blood splashes between the door and piano on the side as shown in photograph No 7.
1786. On the wall between the door and the piano, you mean? Yes.
1787. Can you see them? You can see a small one, but they are very small indeed.
1788. That is a long way off? Yes.
1789. You can see them in No 7 with the aid of the magnifying glass: just under the piano and violin stand. Yes.
1790. There are two angling upwards towards the doorframe? Yes.
1791. Are there only two or are there more? I think there were more to the side of the chair, but I could not find any upon the chair. I expected to find them, but I could not see them. If they are small, they would be difficult to see.
1792. MR JUSTICE WRIGHT: I will hand you this magnifying glass, members of the jury; perhaps you will be able to see them with the aid of that. They are rather small otherwise. (To the witness): If the head was struck of course, the woman would fall forward? Yes.
1793. And after that, she was stuck while on the ground? Yes. I can prove that.
1794. You are coming to that later? Yes, my Lord.
1795. MR HEMMERDE: Can you say how many blows were struck altogether? Twelve, quite definite – eleven; I am sorry. It is rather doubtful as to the front so I have put it definitely as to eleven.
MR ROLAND OLIVER: My Lord, might I be allowed to see all the notes and the sketches this witness made on that evening?
MR JUSTICE WRIGHT: Certainly.
THE WITNESS: There is this one as well, made at the post-mortem.
MR JUSTICE WRIGHT: Never mind the post-mortem.
THE WITNESS: There are three altogether.(ADJOURNED FOR A SHORT TIME.)
1796. MR HEMMERDE: You had just said before the adjournment that you found traces of eleven distinct blows, eliminating one possible one in addition? Yes.
1797. Of those eleven distinct blows, which was the most severe? The one in front in this position. (Pointing).
1798. Did that appear to you to be the first blow struck? It did, for reasons which I shall be able to give.
1799. Will you just give those reasons? The brain substance and small portions of bone I did not find below the head. The other blows on the back of the head, a position which I will describe, must have been produced afterwards, because the striking had produced great pressure upon the inside and had squeezed out the blood, the brain substance and small pieces of brain which lay around.
1800. MR JUSTICE WRIGHT: Just repeat that. You are speaking about the first blow, and you said in that case the brain substance and small portions of bone were not below the head? Not lying beneath it.
1801. Yes, not lying beneath the head; I understand what you meant. Then you said that in the other cases – ? The blows were not so severe; they did not absolutely penetrate the skin. That I found later. The appearance was as if the brain substance and small portions of blood had been pumped out, it is where, the appearance being quite characteristic of their being exuded from the skull.
1802. The blows were not so severe and they did not actually penetrate the skin? Not quite so severe. As we shall see, they smashed up the skull, and in smashing up and driving in the sides of the skull the brain substance exuded through the opening.
1803. Then they did make an opening? The opening was the first opening through which the brain substance and small portions of bone came.
1804. The opening was on the other side up there, and the other blows were round here? No, not on the right. I have the place marked in a small drawing.
1805. They were round the back? Yes, almost the back.
MR JUSTICE WRIGHT: I did not know I was pointing to the right. It was, however, a big blow in front.
1806. MR HEMMERDE: Would you designate where exactly the first blow was (my friend wants to know) on your own head? Just here, exactly in a very similar position (pointing), severing what is known as the meningeal artery on the inside.
1807. How long would it take to inflict these eleven blows? Very quickly indeed. I have an idea of how they were inflicted, but I think they could be all inflicted (I have timed them) in less than half a minute.
1808. How soon do you think death would follow? Death took place almost immediately, to all intents and purposes.
1809. Would the first blow e sufficient to cause death? Yes, quite.
1810. Could you form any view as to what the position of the deceased was when the ten lighter blows were given? Yes, and that explains what I have already described, the pumping of brain substance out.
1811. The head is lying upon the floor when the ten blows are struck? Yes. Lying much in the position as seen in the photograph.
1812. MR JUSTICE WRIGHT: On the ground, but really face downwards, more or less? Yes, my Lord, lying on the right side of the face.
1813. MR HEMMERDE: I still have to return to something with regard to that, but I think it is better to take it now in order. Having noticed the condition of the body, did you see anything of an old mackintosh? I did. There was an old mackintosh bundled up a little beneath the right shoulder of the body. This was taken out and examined and was seen to be partly burnt on the lower right front.
1814. Just hold it up now and let us see where it is burned, and also the bloodstains? And the blood stains?
1815. Yes; this side here, on the right side, and bloodstains here (?) particularly is very characteristic.
1816. MR JUSTICE WRIGHT: Where on the right side? The burning is upon the right side. The bloodstains are all over it.
1817. There were bloodstains also on the right side? Yes, my Lord.
1818. MR HEMMERDE: You said that one of the blood marks was very characteristic? Yes, that is on the left sleeve.
1819. It is inside out now, is it not? Yes. There are several of them by appearances, but his one is very definite.
1820. You have got to the left now? It is the left I am looking for. By the handling a good deal for the blood has been detached – no, it is not; it is quite definitely here. That is the one I refer to, quite definitely here upon the left sleeve, showing a projection mark of blood.
1821. Would you put that into simple language?
1822. MR JUSTICE WRIGHT: What is a “projection mark”? The blood is thrown on to something; it may be small particles of blood projected on to some surface; the usual thing is from a spurting artery. The same thing comes from ink, or anything.
1823. MR HEMMERDE: Some of the blood on that garment might come from the floor, I suppose? Yes; most of it, I think, does.
1824. But you find those traces and you find others of direct projection? This is direct projection. There it is, to speak for itself.
1825. How many are there of those? Only two definite; the other are indefinite.
1826. Have you looked at both sleeves? Yes. I cannot find anything on the other one quite so characteristic. There is definite blood here, but not the characteristic mark of projected blood. There are a good many that are doubtful, nothing that I can speak of definitely.
1827. Just look at the right hand cuff there, outside and in. Do you find anything at all there suggestive? Yes, there is blood upon it, very little blood, in the one part here, and a little here again, but very little. (Indicating).
1828. Just inside? Yes.
1829. And around the outside? Yes, there is some on the outside, but not so much as on the left, I think.
1830. MR JUSTICE WRIGHT: The projected blood on the left sleeve was on the outside? Yes, my Lord, and in this direction too. That is rather important, I think. (The witness indicated).
MR ROLAND OLIVER: If it is not inconvenient, might that mark be shown?
THE WITNESS: It is there. (Handing mackintosh to learned Counsel). There are two marks. May I explain how the direction is arrived at?
MR HEMMERDE: Yes.
1831. MR JUSTICE WRIGHT: Which mark are you talking about now? I will point it out, my Lord, in a minute. It is a mark upon the left sleeve.
1832. Is that the one which you said showed projections? Yes, my Lord.
1833. On the left sleeve where? Just here. (Pointing).
1834. Between the elbow and the shoulder? Yes, my Lord. The greater portion of this is below, and it looks like a streak. A little bit is at the top. It is roughly of the soda-bottle type that can be seen. There is another one by it of the same type.
1835. What does that projection show? Either that there has been a spurting of blood or a splashing of blood in front, presumably by somebody who had it on.
1836. I do not understand; I am sorry. It shows projection? Yes, of blood.
1837. Which the blood took? Yes; that is all one can say.
1838. You mean from a spurt of blood in front of the mackintosh? Yes, on to the mackintosh. I cannot say more than that.
1839. MR HEMMERDE: Supposing that someone had been wearing that? The (?) is the source of the blood from the front, and if anybody (?) wearing this then there had been a spurt of blood from the (?) because it comes in this direction.
1840. Looking at that, the suggestion has been made that the deceased might have thrown it over her shoulders to go to the door and then to have been, I suppose, struck when she had it on? When I saw it, there was no suggestion from the appearance that that was the case.
1841. MR JUSTICE WRIGHT: You mean from the position? Yes, it was tucked under the right shoulder almost in this direction, tucked like that. (Illustrating) There was no suggestion of it having been on the arms whatever, nothing whatever.
1842. MR HEMMERDE: I will leave that then. I will now go back. You had seen that, and then did you proceed to make a careful search of the house for bloodstains? I did.
1843. Did you find any? Yes. I found plenty of suspicious marks but the only one I found was on the edge of the water closet pan in the bathroom.
1844. Have you the photograph there “WHW9”? That small spot shows the position of this blood clot.
1845. Which small spot? The small spot on the pan. It is a little dot on the right hand side of the pan in the front.
1846. Just near that white mark on the pan, is that right? It is on the top.
1847. The one on the right? Yes.
MR JUSTICE WRIGHT: Yes, just about opposite to the water orifice.1848. MR HEMMERDE: Yes, my Lord. (To the witness): You found that. How big was it? Measuring approximately but almost quite accurately, three-sixteenths of an inch in diameter and one-eighth of an inch in height. I measured it. It was difficult to measure the thing without disturbing it.
1849. Was there anything upon it, the actual blood, any streak of any sort? There was a slight streak of blood which can be seen in the photograph in the direction of the pan centre.
1850. Did you have the clot removed after it had been photographed? I removed it myself.
1851. Comparing it with the blood clot by the body, could you come to any conclusion? The conclusion I came to was that the two masses of blood, the small mass and the large one, were about the same time. It is only approximate, but it was not dried blood, it was not very recently spilt blood.
1852. MR JUSTICE WRIGHT: It was about the same time? At the same, time as the blood clot by the body, my Lord. There are certain characteristics.
1853. MR HEMMERDE: Just explain the characteristics? First of all, from examination of the blood below one formed the opinion that it had been spilt for some time. There was exudation of serum and contraction of the blood clot. I examined the blood down below with a lens, and I saw on the outside definitely blood serum which was exuded. You had exactly the same appearance as in the small blood clot on the rim of the water closet pan, but it does not speak very definitely as to time, except that it was not recent. Serum exudation had definitely taken place, and a small central clot had contracted in the same way as it had in the blood below, but it was not dry, there it had been there some time. Those were the tree characteristics; serum erudition, contraction of the blood, and moisture, which gave the similarity to the clot below. It was not dry and therefore in such a position it had not been there for days. It was not recently spilt, because it had lost the characteristics of freshly spilt blood. Beyond that I cannot go.
1854. Was it you who found it? Yes, I found it.
1855. Was the place where it was found in any way obscured? I did not notice it for a good while because the gas was low and it threw a shadow. This is a distorted photograph, and it does not convey quite the idea. The gas is to the right of the window, and it throws a shadow over the pan, over this side of the WC pan and it is quite in the shadow, quite dark.
1856. You can see it again in No 13? I only found it on close examination with a pocket torch.
1857. At any rate, it was in the shade and you had at first missed it? Yes, I did not see it at first.
1858. Did you subsequently make a post-mortem examination? I did, the next day, between twelve and two.
1859. You have stated, I think, a certain amount of what you found then. Perhaps you had better state shortly what you found? The woman measured 5 ft 3 ins or 5 ft 4 ins, slightly built and a prominent abdomen. There was no evidence of pregnancy, no evidence of former pregnancy. The external genital orifice was quite clean.
1860. No evidence of blood? No. There was a small recent bruise mark on the left side of the left upper arm.
1861. I think you have already given the evidence as to the other things. Was there any evidence of menstruation? None whatever. There was no other external marks of violence on the trunk or the limbs.
1862. MR JUSTICE WRIGHT: Was the bruise anything you attach importance to? No, my Lord, nothing at all.
1863. MR HEMMERDE: Did you find anything else in the bathroom apart from this clot? No.
1864. There are other matters which you have mentioned. I think you made a biological examination of the blood clot? I did.
1865. MR JUSTICE WRIGHT: What was the result? It was typical of human blood, red corpuscles and white corpuscles. I applied the usual test and it gave very definitely the precipitant test for human blood.
1866. It was human blood? Yes.
1867. That is all you can say about it? Yes, that is all.
1868. MR HEMMERDE: Can you say definitely it was not some menstrual blood? It was not an early menstrual blood, and I do not think it was menstrual blood at all.
1869. Did you find anything else in the bathroom at all? Yes, I found on the edge of the bath a nailbrush, which I examined. This is the brush. (Indicating). The fibres were moist, and the wood had the appearance of just drying after having been used some time before.
1870. But you found no evidence of blood on it? No. I am not prepared to state how long before that had been used.
1871. Would it want a very heavy instrument to have caused that fracture, the first blow? Fairly heavy, yes.
1872. Have you seen this, which was produced this morning? Yes.
1873. Just look at it. (Iron bar handed to witness). Yes, just such a weapon. If a blow was made with this it would produce the appearances I found, or such a weapon would.
MR JUSTICE WRIGHT: Has this been exhibited?
1874. MR HEMMERDE: Yes, my Lord: it is Exhibit 55. (To the witness): In your view that is just the sort of weapon that might have done it? Yes.
1875. When you arrived there, did you see the prisoner? I did.
1876. How soon after your arrival? Immediately.
1877. How long were you there altogether? Till after one o’clock.
1878. For three hours? Yes, for three hours.
1879. Was he there all the time? No, he left. He went down to the police station, and then I went down to the police station afterwards.
1880. A good time, was it? Yes. The time of arrival, I can be definite about, but not the time I went away.
1881. Can you tell my Lord and then jury what was the demeanour of the accused when he was there? I was very much struck with it: it was abnormal.
1882. In what way? He was too quiet, too collected, for a person whose wife had been killed in that way that he described. He was not nearly so effected as I was myself.
1883. Do you happen to remember anything particular that led you to that conclusion? I think he was smoking cigarettes most of the time. Whilst I was in the room examining the body and the blood he came in smoking a cigarette, and he leant over in front of the sideboard and flicked the ash into a bowl upon the sideboard. It struck me at the time as being unnatural.
1884. To do that would he have to lean across anything? He did not come forward. I can recall his position at the moment: he leant forward so as not to step on the clot.
1885. About this question of the clots of blood of which you have spoken, have you, professor, had very great experience on this matter of clots of blood? Yes.
1886. Have you been in very many cases of this sort on one side or the other? Yes, a good deal more than 100, perhaps. I have been doing this sort of examination for over thirty years.CROSS-EXAMINED BY MR ROLAND OLIVER.
1887. You were a Police Surgeon before you had your present position? I am still a Police Surgeon.
1888. Your are still? Yes.
1889. I want to begin with the last bit of your evidence. May I put in this before that? You have not had the position of these blows put in and I have a note I made at the post-mortem showing the position. I have not given the position I found at the post-mortem examination, which is very important.
1890. MR JUSTICE WRIGHT: You have a sketch? This I made as I was making the post-mortem examination. It shows the position after the hair was removed and the head shaved. It shows the cuts.
MR ROLAND OLIVER: I do not want to stop anything, but how can that indicate who did it?
MR JUSTICE WRIGHT: No, of course not.
MR HEMMERDE: The Professor thinks it important I hesitated to ask him.
MR JUSTICE WRIGHT: Counsel must conduct the prosecution and he will ask you or not ask you as to anything that occurred.1891. MR HEMMERDE: Can you give quite shortly, what your reason is? I can. I formed an idea of the mental condition of the person who committed this crime. I have seen crimes, many of them of this kind, and know what the mental condition is. I know it was not an ordinary case of assault or serious injury. It was a case of frenzy.
MR JUSTICE WRIGHT: We may have already formed that opinion. Where blows are struck by anyone that probably does produce frenzy but that is a matter for the jury.1892. MR ROLAND OLIVER: With reference to the last matter, you have noticed that my client has been under medical observation as to his mental condition ever since his arrest? I know that he will have been.
1893. If there is anything to be said about his mental condition there are people competent to say it who have lived with him? Yes, I do not wish to express any opinion.
1894. If this is the work of a maniac and he is a sane man he did not do it. Is that right? He may be sane now.
1895. If he has been sane all his life and is sane now it would be some momentary frenzy? The mind is very peculiar.
1896. It is a rash suggestion, is it not? Not the slightest. I have seen this sort of thing before, exactly the same thing.
1897. Rash to suggest in a murder case, I suggest to you? I do not suggest who did it at all.
1898. The fact that a man has been sane for 52 years and has been sane while in custody for the last three months would rather tend to prove he has always been sane, would it not? No, not necessarily.
1899. Not necessarily? No, we know very little about the private lives of people or their thoughts.
1900. I want to deal with the evidence and not speculation. You asked me, I think.
1901. Let us go back. You have told the Jury that you were very much struck with his demeanour. You noticed it at the time and were very much struck with his callous demeanour? I was.
1902. Why did not you say so at the Police Court? Because I was not asked.
1903. You do not mind volunteering things. You have been volunteering things for the last five minutes. There is a great deal I would like to volunteer that my Lord has pulled me up on.
MR JUSTICE WRIGHT: I am not conducting the case for the Prosecution or the Defence. It is for Counsel for the Prosecution and Counsel for the Defence to ask questions that are proper and appear to them to be desirable from either point of view.1904. MR ROLAND OLIVER: I will get this fact from you: Not one word about his demeanour was said by you at the Police Court? No.
1905. And although you gave evidence for a long time and in detail? Yes.
1906. Now, a question or two with regard to the probable position of this poor woman when she was killed. I understand you to say, and if I may say so I am accepting it, that at the moment of first impact her head was somewhere in the neighbourhood of the left hand side of the fireplace and that chair that stands in the corner? Yes.
1907. Which two things are, of course, quite close together? Yes.
1908. Do you know that the bottom of this woman’s skirt shows a mark where it was upon that gas fire? I do not.
1909. There is evidence, if you will take it from me, given by the Police that there are three characteristic burn marks on the lower part of the skirt corresponding with that gas fire which would indicate that the gas fire had been alight, would it not? Yes.
1910. You see the handle to the gas fire is on the right hand side of it? Yes.
1911. And just above it is a gas light? Yes.
1912. Suppose a woman went into that room, lit the gas and lit the fire, she would have to stoop down, would she not? Presumably, yes.
1913. If she did that with her back towards the doorway and someone was on her right hand side he would be in a position to strike her as she rose? He would.
1914. And her head might well be in the very position in which you put it? Exactly.
1915. Let us see if that is quite true. You have suggested she might have been sitting in the armchair? Yes.
1916. The jury can look at that. You see upon that armchair in the corner a violin case? Yes.
1917. And on that violin, case large splashes of blood? Yes.
1918. It was on the chair when she was struck, was it not? Yes, the violin case.
1919. The violin case was on the chair when she was struck? Yes.
1920. That does not much suggest she was sitting in the chair? Yes, it does. I have said she would be leaning forward.
1921. There was room here for two chairs? But you will see on the wall blood splashes and the body would intervene.
1922. You have agreed with me the suggestion is a possible one? Yes.
1923. Your suggestion was she was in the armchair? It brings the head into the same position in both cases.
1924. Will you tell me how bloodstains got on the violin case? There is a direct line open between her head and the blood patches. It can be seen to be falling.
1925. She is struck in front? Yes, the blow goes up.
1926. It goes out sideways and the violin case is behind her? Yes.
1927. Whereabouts where the blood splashes on the violin case? They would be on the top.
1928. They go right along, do not they? Yes.
1929. If she had that coat round her and the gas fire was alight and she fell when she was struck so as to burn her skirt in the lit fire, do you not think it is quite possible that that mackintosh swing around on to the fire place and caught fire? No, because there is no evidence of it having been on her right or left arm.
1930. Suppose it was round her shoulders and she collapsed, do you not see the possibility of the bottom of the mackintosh falling into the fire and getting burnt too? There is that possibility.
1931. Her hair was pulled away from her head, was it not, all up? Yes.
1932. And the pad which had been under her hair was away from her body? Yes, some inches.
1933. Do you not see the possibility of someone having grasped her by her hair to pull her from the fire? Yes.
1934. Where her clothes were burning? I do not know about the burning.
1935. It is said that my client tried to destroy the mackintosh by burning it because it was his? That would take time would it not? I am not an authority on the burning of mackintoshes.
1936. Then we will leave that to our general knowledge. Now to come to another matter. The theory has been put forward here by the Recorder when he opened this case that this might have been done by a naked man wearing a mackintosh? I heard that theory, yes.
1937. Whether clothes or whether naked it would be necessary, would it not, in all common sense that many splashes of blood would fall upon the assailant? Yes, I should expect to find them.
1938. When the blood vessels are broken as in this case they fly out, do not they? Yes.
1939. Would you agree that nothing in this life is certain, but it is almost certain the assailant would have blood on his face and his clothes? On his left hand, I think he would.
1940. What about his right? No, I don’t think so.
1941. Think of it running down? No. You do not find the blood so much on the hand that holds the weapon.
1942. Not when blow after blow is delivered? No. If it is done by the person’s getting hold of the victim by the hair there would be a great deal of blood upon the left hand and not upon the right.
1943. The last blows being probably struck with the hand on the ground there would be blood upon his feet and lower part of his legs for certain, would not there? I should expect that.
1944. And the blood would continue to spurt while these blows were being struck, would it not? Yes, and I looked for it.
1945. So that the mackintosh would never come down below the knees of this man, who would leave his leg from the knees downwards exposed to the blood? Yes.
1946. Whether he was wearing trousers or whether he was wearing nothing? Yes.
1947. MR JUSTICE WRIGHT: So there would be some on his face? There would be some on his legs.
1948. MR ROLAND OLIVER: And his face? Yes.
1949. And his hair? Yes, but more likely upon the face.
1950. You agree it would be most likely on the face? Yes, I agree.
1951. Although not so certain to be on the leg? Yes, that is right.
1952. With regard to the fingernails you would agree, would you not, if blood gets below the finger nails it is difficult to get away? It is difficult.
1953. It really is difficult? Yes.
1954. Would you agree it would be almost certain that the assailant would have blood under the fingernails? Not necessarily.
1955. Through handling the thing as suggested? Touching things unless you scrape the things you would not get blood under the nail.
1956. They had to lift the mackintosh up? No, the mackintosh was not underneath the body. There was a little underneath the right shoulder when I saw it.
1957. Somebody who saw it before you has told us quite clearly it was under the body with bits of it sticking out. But putting it where you saw it, it must have been thrust under the body? But I understand nobody had taken it out before I saw it. I do not think anybody removed it before I saw it.
1958. You agree you do not know what happened before you saw it? True.
1959. Assume it was under the body that would mean that the assailant if he wore the mackintosh lifted the shoulders up and put the mackintosh underneath. That would involve getting heavily dabbled with blood? No, when I saw it there was a little pushed under the shoulders by a hand.
1960. Supposing the mackintosh were put under the body the assailant would have had to lift that shoulder and the hand up to do it? He would.
1961. That would have involved getting heavily dabbled in blood, would it not? Dabbled in blood but not heavily. Supposing he did?
1962. I ask you to assume it. You can assume a thing without admitting it? Yes.
1963. When you went to the bathroom, it was suggested that the Defendant went and had a bath. Did you see any signs of a wet bath towel? No, I did not.
1964. Or a wet towel of any sort? No.
1965. MR JUSTICE WRIGHT: There was no towel in the bathroom. As far as I remember, there was not, my Lord.
1966. MR ROLAND OLIVER: I am told there was a towel. There may have been one.
1967. One may take it, it was certainly dry and you would have noticed it because you were on to the nailbrush? Yes, that is why my attention was concentrated on that.
1968. MR JUSTICE WRIGHT: Was that towel dry? It had not the appearance of a person having recently taken a bath. There was no suggestion to me of anyone having recently taken a bath.
1969. It did not appear so to you? No, not within the last hour or so, my Lord.
1970. MR ROLAND OLIVER: The person who did it got himself washed somehow as far as you could see? I cannot say. It was a long time, 4 hours.
1971. Was the suggestion that he was naked ever made before this Court? I do not know.
1972. You never heard it? Yes, I have heard it.
1973. But you have never heard it made in public before? No.
1974. Let us go to the mackintosh for a moment. You have pointed out to the Jury two things which you say are definitely blood projections? Yes.
1975. Will you take it up again? (Same handed). You told the Jury (do not take it I am differing from you for a moment) that what you would call a trickle would come around sideways, an elongation, something like that? Yes.
1976. It would be splashed, spurted or dropped? Yes.
1977. Are those two marks there anything more than a drop from the head on to that mackintosh? Not necessarily. It all depends upon the condition. I can fall in with your suggestion putting the mackintosh in the position (illustrating) and the blood dropping down there would produce that effect.
1978. First of all, I got it from you that these marks on the sleeve might be the marks of a drip? They might.
1979. What I am suggesting to you is that they are perfectly consistent with marks of a drip if that Sleeve happened to be in a position which would catch the drip in that way? They are.
1980. Now beyond those two there is nothing on that mackintosh that you can show which points definitely to anything being a stain or a drip? No.
1981. Having regard to your evidence that there was a horrible spurting while this dreadful thing was going on, do not you think that mackintosh would have more marks on it than that? You mean if the person assaulting the deceased had worn it would there have been a lot of blood upon it?
1982. Yes, supposing he was wearing it and there was this frightful spurting you have told us about, do not you think there would be more than those two things upon it? No.
1983. Why do you say that? Because the blood all goes towards the floor.
1984. You have pointed out to the Jury it has been spurting all round the room? That was the first blow.
1985. You told me while she was lying on the floor the blood would spill? Yes, it would as it pumped out.
1986. And you said you would not expect any more than those two marks? Yes, there would be a great deal.
1987. Typical splashes is my question? They do not always fall as typical splashes. There is plenty of blood here which might have been projected and which bears the typical appearance; they do not all bear the typical appearance.
1988. Photograph No 6 shows that 4 ft from the ground level with the fireplace a whole series of splashes. There has been a regular spurt there? Yes.
1989. Which shows where the head probably was when it was hit? Yes.
1990. That is rather at a height above the ground which would bring them away from the assailant? Level with the hand of the assailant.
1991. And all around? No, I tried to prove it. They all went into the corner.
1992. You find blood splashes well above the floor all round the room over the piano? In that direction.
1993. That is the opposite direction to the corner where we are now? No, I think those blood splashes by the door did not come from the first blow.
1994. They went upwards did they not? Yes, from the floor.
1995. Then while the head was on the floor, the blood would go upwards? Yes, and away from the assailant.
1996. You are speculating? I am.
1997. You are simply guessing? No, not guessing.
1998. It depends entirely where he stood? Yes, it does.
1999. Very well, I have put my case to you on that. Now with regard to the time of death. When did you first think the time of death was important? Immediately I examined the body.
2000. That was your first thought? It was a thought.
2001. One of your first thoughts? I thought “How long has this woman been dead”.
2002. And that you proceeded to ascertain by a series of observations, first as to rigor-mortis and, secondly, as to the condition of the exuded blood? The blood is a (guide) but not as definite as rigor-mortis.
2003. You put rigor-mortis first but the other did assist you to form your opinion? It did.
2004. How many notes did you make with regard to rigor-mortis? Practically none, I think.
2005. Can you show me one? I do not think I can.
2006. Where did you make them? I made these in the room.
2007. I asked you before lunch, do you remember, to give me all the notes you made in the room? I have got them here; I am not going to claim any others.
2008. Are there any notes on these papers with regard to rigor-mortis? There are not.
2009. It comes to this, does it not, that you being intent from the start on the importance of rigor-mortis as to the time of death have not made one note with regard to rigor-mortis? That is so.
2010. Your colleague said on another occasion every quarter of an hour you examined the body for the progress of rigor? Yes, I was constantly observing it.
2011. You would agree would you not, that the progress of rigor from the point of view of crime is important, I mean the stages that are reached during your observations are important? Very.
2012. And not one note made? No, but I know definitely.
2013. Let us take the question of rigor. Rigor is a very fallible test as to the time of death? Not in the present case of an ordinary person dying in health.
2014. It is a very fallible factor even in healthy people? It is, just a little.
2015. Not just a little. I am putting very? No, not very fallible.
2016. Does it depend, amongst other things, upon the muscularity of the person? It does.
2017. And the powerful and muscular body will be affected by rigor much more slowly? Yes.
2018. Than a feeble and frail body? Yes.
2019. Was this a feeble and frail body? Yes. She was not exactly frail; she was a feeble woman.
2020. You have used the word “frail”? Yes, she was a weak woman.
2021. Frail? Yes, frail.
2022. It is your own word? Yes, my own word.
2023. Then we may summarise your last two answers and it comes to this, that she was a woman who was likely to be quickly affected by rigor? No, she would be rather delayed if anything.
2024. MR JUSTICE WRIGHT: I thought you said it would be quicker in a frail person and slower in a person of muscularity? She would be delayed.
2025. MR ROLAND OLIVER: Do you wish to say that a feeble and frail person would have delayed rigor? No.
2026. Why do you say it then? She was in a condition of good health although a frail woman.
2027. Then I will start all over again. A muscular body would take longer to be affected by rigor than a feeble and frail body? Yes.
2028. Was this woman a feeble and frail body? Yes.
2029. Then she would be likely, would she not, to be more quickly affected by rigor? A little.
2030. Then why did you say rather longer just now? Not rather longer than a muscular person.
2031. You are not arguing the case are you? No, I wish to state what I found.
2032. You know what is at stake here? I do.
2033. Bearing in mind that this feeble and frail woman would be more likely to be affected by rigor, are you going to swear she was killed more than 3 hours before you saw her? No, I am not going to swear; I am going to give an opinion and I swear that the opinion that I give shall be an honest one.
2034. MR JUSTICE WRIGHT: then what is your opinion? My opinion was formed at that theme that this woman had been dead about 4 hours.
2035. MR ROLAND OLIVER: Now that I have reminded you that she being feeble and frail rigor would come on quicker, does that move your opinion? No.
2036. It does not? No.
2037. You do not think she was killed 4 hours before you saw her? I do.
2038. You do? Yes.
2039. That is your honest opinion? Yes.
2040. You saw her at 10.10? Yes.
2041. So if she was alive at half past 6 your opinion is wrong, is it not? Yes.
2042. Does not that convince you what a very fallible test rigor mortis is? No, it does not. I am still of the opinion.
2043. Do you think the milk boy imagined seeing her alive? I do not want to think about the milk boy and what he saw at all.
2044. Let us take other things about rigor. It starts with the neck? It starts with the face.
2045. And then the arms? Yes.
2046. Was one arm affected more then another? Yes.
2047. That is unusual, is it not? Yes, but you do find it.
2048. Does it pass down the trunk and finally down the legs? Yes.
2049. Both legs together? No, not the two legs together.
2050. Not as a rule? No, you usually find one arm more set in rigor than the other. It does not come on exactly like a wave.
2051. Was the process over by 1 o’clock? Not quite. The left leg was not very rigid. Its progress was slow and that helped me in judging the time.
2052. MR JUSTICE WRIGHT: The left leg was still not quite stiff? No, my Lord.
2053. MR ROLAND OLIVER: Had the rigor progressed at all by 10 minutes to 11? Yes, but if you keep on testing the limb to see whether rigor mortis is present you make it flaccid again and you do not get quite a result. Testing it destroys the evidence.
2054. You were testing it about every quarter of an hour? I do not think every quarter of an hour.
2055. The other doctor said every quarter of an hour. Is that right or wrong? It was fairly often.
2056. Had the condition progressed; what was the condition at 10 to 11? I did not make any notes as we went along of progression.
2057. Not making notes! You have a good memory, I suppose? I have.
2058. What was the position? It had got to the right shoulder.
2059. By 10 to 11? By 10 to 11.
2060. I am putting 10 to 11. Is that all? I was not looking at the times as I went on. I did not take the time on any other occasion except when I went to the house.
2061. Surely if your memory does not help, you, as a scientist, will be able to help me. How much progress would rigor make in two hours, 8 to 9 and 10 to 11?
2062. MR JUSTICE WRIGHT: In one hour? In one hour after I saw the woman?
2063. MR ROLAND OLIVER: I was putting the question under a misapprehension. How much in one hour? Do you mean one hour after I saw the body?
2064. No. May I start again? May I alter my question and say, to what condition had it got by 10 to 12? I should say it had got well down the right arm and possibly beginning in the right thigh, but I should not be sure of the time.
2065. One other thing you relied upon in forming your estimate of time and that was the condition of the blood. You say it was only corroborative and you do not base yourself upon it. With regard to the blood, would it be right to say that when you first examine the blood there was a small amount of serum exudation? Yes.
2066. A small amount? Yes.
2067. And so that the jury may follow, serum is a yellowish substance which gets squeezed out of blood? Yes.
2068. A sort of liquid. The blood congeals in clotted form and serum squeezes out. Yes.
2069. And you say there was only a small amount. Let me suggest that is indicative that death had taken place long before? Very little serum exudes over the first few hours.
2070. Very well. I have put my case to you. How long does blood take to become clotted? It varies very much. I varies a little bit but not much in 5 or 6 or even 10 minutes.
2071. And its first condition when clotted is very mobile? Yes.
2072. It will just retain a clotted shape but if interfered with will break up? Yes.
2073. May I call a 10-minute-old clot very new? Yes.
2074. If you interfered with that it would break up, would it not? Yes.
2075. Or splash would it not, and may I suggest to you it would take at least an hour for a clot of blood to be solid enough to become what I call interfered with and manipulated, do you agree with that. No.
2076. How long do you say? It would take a clot of blood solid enough to be interfered with? I do not quite understand what you mean by “interfered with” – lifted about, moved?
2077. Not moved, let us say dripped on to a hard substance. I see, to be carried by being touched and adhering to something.
2078. I suggest it would be at least an hour before you could take a clot and drip it down on to a table without smashing it. A clot would smash up even then.
2079. It would break up unless it was quite solid? Yes, there would be some evidence of it being thrown in one direction.
2080. You see, what we describe as a fresh clot if you dropped it on to something it would become liquid or break up and splash? Yes, it might.
2081. What I want to put to you is it would be at least an hour before a clot of blood could be dropped without losing its shape after it has struck a foreign substance. Do you agree? I do not quite catch your meaning. Would it take at least an hour before it would lose its shape?
2082. Let me take a clot of blood three-sixteenths wide and one eight of an inch high; while it is fresh and newly clotted, if you were to drop that on to a lavatory pan it would give out, would it not? It would show some signs of spread out.
2083. Experiments have been made about this? I have made a good many myself.
2084. What of, dropping a clot? Yes.
2085. What I am putting to you is that it would take at least an hour before a clot of blood would be sufficiently solid not to flatten when it was dropped on to that lavatory pan? No, I do not agree.
2086. You do not? No.
2087. How long do you say it would take? An hour. If you took the surface of a clot upon your finder and knock it down it would fall off complete almost.
2088. Considering the blood you have described on the edge of that pan what I am putting to you is that that must have dropped upon the pan at least an hour after that woman met her death. No, I do not think so.
2089. Why do you not think so? Because it is quite fresh blood.
2090. It has not lost its shape; it has not flattened out or become fluid. I do not think it had been dropped from a great height. It does not show a splash to the side and the photograph shows it too.
2091. Would that top of that pan be moist? Yes, almost certain to be; they always are.
2092. With a little film of moisture? Yes.
2093. Would not that cause the blood to run a little bit? No. This is not running blood. It shows quite definitely it is a splash, as you say.
2094. I never called it a splash, a slight smear you said? Slight smear I said.
2095. It has not affected the shape of the clot; it remains conical. What I am putting to you is that smear of blood would be caused by the blood being moistened by the moisture on top of the pan? No, it is too far; it is twice the length of the piece itself.
2096. If it was flung it might go to anything. It is only in one direction? Yes.
2097. Is that towards the centre of the pan? Yes.
2098. That, I suppose, is the way the thing had tilted? Yes.
2099. Showing it had run downhill. Did you get blood on your hands while you were examining this body? Very little.
2100. Did you wash them? No, not until I got home.
2101. When you, for instance, tested the head for rigidity of the neck, could you avoid getting blood on your hands? I had very little. I had a little, but very little.
2102. When you were manipulating the limbs of the poor thing, you were in contact with it practically? Yes.
2103. You never saw that clot of blood until you had been in the bathroom sometime, did you? Not for five minutes.
2104. You told us you missed it at first? I did not see it at first.
2105. Does it occur to you that someone who came in after 9 had dropped that clot of blood on the pan? That possibility did occur to me very much indeed.
2106. Does it occur to you now? It does.
2107. Having regard to the fact that there is no other blood up the stairs at all, none, if a man went up all, bloody to wash himself it would be an amazing thing, would it not, that there was no blood upstairs. Only the one clot.
2108. Having regard to the state of that clot and your agreement with me it was probably an hour after that it fell? I think you agree that? But I do not rely much for the time on the clot.
2109. Will you accept it from me; indeed, you said the chance was that the police had carried it up there? Yes, I thought the police might have dropped it there.RE-EXAMINED BY MR HEMMERDE.
2110. That occurred to you, Professor, because it was the only clot of blood upstairs? The only mark and it is so striking.
2111. MR JUSTICE WRIGHT: And you now think it may have been carried there by the police? No, my Lord.
2110. I thought you said so? I was asked, did I recognise the possibility and I said I did recognise the possibility and made enquiries about it.
2111. MR HEMMERDE: It was only a possibility present to your mind? Yes, I recognised the possibility.
2112. MR JUSTICE WRIGHT: It is a possibility? Yes, certainly, but I took care to find out that the police had not been up.
MR ROLAND OLIVER: I meant the witness to understand that it was he who might have done it.
THE WITNESS: I myself?
MR ROLAND OLIVER: Yes.
THE WITNESS: I am glad you have said that. No, I did not.2113. MR HEMMERDE: So far as you are concerned, have you any doubt about it? Not the slightest doubt about it.
2114. MR JUSTICE WRIGHT: The suggestion is that it could not have been carried up at once by the murderer. That is the suggestion I would like to know what you would say about that. I thought at one time you were disposed to agree it could not have been carried up there, fresh blood, by the murderer? My idea was it was fresh blood carried almost immediately upstairs. How it came to be there, I do not know.
2115. MR HEMMERDE: Can you draw distinction between clots of blood and drops of blood? No, a drop of blood will become a clot; it is the same thing. Do you mean blood transferred as a clot?
2116. Yes. At any rate, you think it is possible that was carried up at once by the murderer? Yes.
2117. MR JUSTICE WRIGHT: If that was so, why did it remain in that very concentrated form and shape and why did it not spread? Because it was coagulating. The opinion I have is that it was almost in the condition of cool blood when it was dropped and it had not fallen from a great height.
2118. If it fell from a great height, would you expect it to spread? Yes.
2119. If it falls from a small height, you mean it might not? Yes. That is what you put to me.
2120. With regard to rigor mortis, if the body is dressed and not prepared after death, does that affect the time rigor mortis will take? Very little actually.
2121. But it does affect it a little? It affects the temperature of the body.
2122. MR JUSTICE WRIGHT: You are being asked about rigor mortis. No, it has no effect upon rigor mortis.
2123. MR HEMMERDE: When you formed, your opinion as regards the time it would take you formed your view with reference to the actual body before you there? I did.
2124. With all the action of fragility and feebleness, and so on? Yes.